11. Visualizing Piece-wise Uniform Distributions
Visualizing a Piece-Wise Continuous Probability Distribution
Now it's time for a challenge!
After Sebastian introduced a uniform continuous probability distribution, he then showed you a piece-wise continuous function representing the probability of when someone was born. You are going to code a generic piece-wise continuous probability density function in Python.
Your result is going to look something like this:
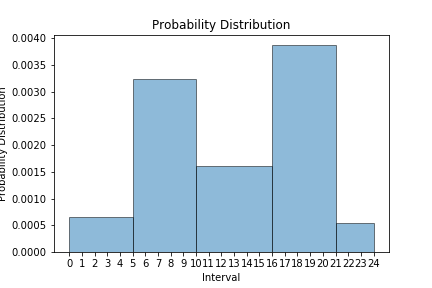
Instructions
Write a function that, given a list of x-axis intervals, relative probabilities and a total probability, calculates the height of each bar. Remember that the sum of the area for all bars should be the total probability.
Here is an example input and output based on the above visualization:
- a vehicle accident is 5 times more likely from 5am t
o 10am versus midnight to 5am. - a vehicle accident is 3 times more likely from 10am to 4pm versus midnight to 5am.
- a vehicle accident is 6 times more likely from 4pm to 9pm versus midnight to 5am.
- a vehicle accident is 1/2 as likely from 9pm to midnight versus midnight to 5am.
- The probability of getting in an accident on any given day is .05
The inputs would look like this.
For the hours, you can use 24 hour time
hour_intervals = [0, 5, 10, 16, 21, 24]
relative_probabilities = [1, 5, 3, 6, 0.5]
total_probability = 0.05
The output would be the height of each bar:
[0.0006451612903225806,
0.0032258064516129032,
0.0016129032258064516,
0.003870967741935484,
0.0005376344086021505]Hints
- Summing the area of all the bars equals the total probability, which in this case is 0.05.
- The relative probabilities and total probability can be used to find the exact area of each bar. If the area of the first bar is A, then the area of the second bar is 5A, the third bar is 3A, etc.
- Once you know the area of each bar, you can divide each area by its width to calculate the bar height.
But the function should be generic. It should be able to receive an arbitrary list of numbers with the relative probabilities of each interval and any value for total probability. Before trying to write the program, it might be helpful to calculate the results you expect with a pen and paper. That will help you work through the logic of the programming.
You'll find the exercise in the next part of the lesson.